

LAATSTE
ZES AFLEVERINGEN
265. HORROR-TANDARTS (12/12/2021)
264. DOORGEZAAGD
EN GEPHOTOSHOPT: AELBERT CUYP IN DORDRECHTS MUSEUM
(07/11/2021)
263. ONTMOETING
MET KRIJN, NEANDERTHALER
IN DOGGERLAND (03/10/2021)
262. HERMAN
STOK, DE EERSTE ECHTE DJ; OF: WAAR IS GUDRUN JANKIS GEBLEVEN?
(06/06/2021)
261. DE PEST
(IN); TENTOONSTELLING IN
HET
VALKHOF, NIJMEGEN (23/05/2021 en 08/08/2021))
260. BILABIAAL;
OF: HOE KLONKEN DE GEBROEDERS DE WITT? (18/04/2021)
De rubriek FHM's A-viertjes
verschijnt onregelmatig. Maar als hij verschijnt, doet hij dat op
zondag.
![]()

William Farr (1807-1883), voorloper van de corona-grafiekentekenaars
The Popular
Science Monthly vol. 23, 1883. Maker onbekend.
Overgenomen van Wikipedia (E); William Farr.
Grafieken, ik heb er nog nooit zoveel gezien als tijdens de zich
nu al 2 jaar voortslepende coronapandemie. Ik noem het ook wel eens: de
grafiekencrisis.
Ik schat dat ik sinds het begin van de corona-ellende
gemiddeld toch zeker een uur per dag getallen en vooral veel grafieken heb
zitten te bestuderen. Daar moet ik dan maar chocola van zien te maken, als alfa
(die op school altijd wel redelijke cijfers behaalde voor wiskunde, OK, maar
dat is wel een halve eeuw geleden).
Grafieken van aantallen positieve testen, aantallen opnamen
in een ziekenhuis, aantallen patiŽnten die op de IC beland zijn en aantallen
overledenen. Op de voet volg ik op Twitter de corona-rekenaars en -duiders Marino van Zelst, Yorick Bleijenberg en vele anderen. Door alle getallen vergeet
ik nog wel eens dat het om mensen gaat.
Coronagrafieken hebben een vervelende eigenschap. Ze beginnen
doorgaans vrijwel horizontaal, heel kalmpjes, maken zich daarna langzaam maar
zeker los van de X-as, om vervolgens ineens als een vuurpijl de lucht in te schieten.
Plotseling een angstwekkende stijging van het aantal nieuwe ziektegevallen,
gevolgd door die van de ziekenhuisopnames en erger.
Dat komt doordat het aantal gevallen (aanvankelijk) exponentieel
stijgt. Als dat beruchte R-getal, de reproductiefactor, bijvoorbeeld 4 bedraagt,
verviervoudigt het aantal besmettingen elke 5 dagen. Zijn er vandaag 1000
nieuwe gevallen, dan zijn er over 5 dagen 4000, over 10 dagen 16.000, over 15 dagen
64.000, over 20 dagen 256.000…. Al snel is de Y-as te kort om het aantal nog
weer te kunnen geven.

Vooral de omikron-variant verovert de wereld met extreem hoge
snelheid. Over een paar weken honderdduizenden besmettingen per dag in
Nederland, miljoen in de UK en straks een slordige 3 miljard in totaal mondiaal;
zulke voorspellingen lees je wel.
Er zijn twee reacties mogelijk op zulk nieuws. Optimisten en
wappies roeren zich vooral in de fase dat de lijn nog bijna horizontaal loopt. Wat
maken mensen zich nou druk om 100 omikron-gevallen in Nederland? Goed, eergisteren
waren het er nog maar 50, maar dat betekent dat er nog maar 50 zijn bijgekomen.
Zwaar overdreven, vinden ze dan, dat we in intelligente lockdown moeten en niet
eens meer op ferkansie naar Oostenrijk mogen om te skiŽn, voor die paar mensen
met zo’n griepje.
‘Snap je nou nog steeds niet dat het exponentieel gaat?’, is
dan de reactie van degenen die met angst en beven wachten totdat die lijn
ineens de vorm van een hockeystick gaat aannemen. Wat onvermijdelijk gaat
gebeuren. Honderden besmettingen worden er duizenden, worden er tienduizenden.
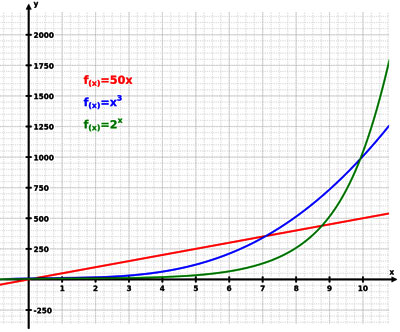
De groene lijn is van een exponentiele functie en piekt heel
snel
Overgenomen van Wikipedia; Exponentiele groei
Maar hoever kun je die lijn doortrekken? In Noorwegen becijferde
iemand dat er ergens begin januari 300.000 besmettingen per dag te betreuren
zouden zijn in dat land. Dat zou een afschuwelijke ontwrichting van de
maatschappij teweeg brengen. Maar het voordeel zou wel zijn dat de Noren dan
binnen 3 weken van corona af zijn, want Noorwegen telt maar iets meer dan 5
miljoen inwoners.
Zo’n exponentiŽle groei kan echt niet tot in de eeuwigheid
doorgaan. Neem bijvoorbeeld het verhaal van die graankorrels op een schaakbord.
Volgens een bekende legende zou de uitvinder van het
schaakspel een beloning van de koning van India (of China, of PerziŽ) gekregen
hebben. Die bestond uit ťťn graankorrel (of rijstkorrel, maar dat maakt in
principe geen verschil) op het eerste veld van het schaakbord, 2 op het 2e, 4e
op het 3e, 8 op het 4e, 16 op het 5e, enzovoort. Op elk veld telkens het
dubbele van het vorige veld.
Hoeveel graankorrels komen er dan op het 64ste en laatste veld?
Veel meer dan erop passen. Zelfs veel en veel meer dan er graankorrels op de hele
wereld zijn. Het zijn er 9 triljoen en nog wat, een getal met 19 cijfers, ruim genoeg
om de wereld voor de eerstkomende tig miljard jaar te voeden.
Dus dat verhaal met dat graan, dat houdt een keer op. Al
beginnen ze met graankorrels, en komen ze daarna met zakken graan en daarna met
complete goederenwagens vol graan; ooit komt er een einde aan het aantal
graankorrels dat ze bijeen kunnen brengen.
Of neem die verneukeratieve piramidespelen en kettingbrieven
(zie de Wikipedia) die de deelnemers gouden financiŽle bergen beloven. Iedereen
die inhaakt, moet entreegeld betalen aan iemand die al eerder is ingestapt.
Vervolgens moet hij, om de geldstroom op gang te houden, 4 nieuwe deelnemers
werven, die er ook weer 4 werven, die er ook weer 4, etc.
Dat is het kenmerk van alle exponentiŽle stijgingen. Theoretisch
gezien kunnen ze tot in het oneindige doorgaan. Maar in de praktijk keert de
wal ooit een keer het schip.
De aller-somberste voorspellingen over corona komen daardoor
gelukkig ook nooit uit. Jaap van Dissel van het RIVM profeteerde begin dit jaar
dat de alfa- (‘Britse’) variant in Nederland snel zou gaan zorgen voor 170.000
nieuwe besmettingen per dag. Maar zover kwam het lang niet. En achteraf had hij
het natuurlijk niet zo gezegd, en zeker niet zo bedoeld.
Laatst stuitte ik op een bijzonder verhaal over dit soort
zaken. Een arts uit Londen, ene William Farr, hield al in 1840 statistieken bij
van sterftecijfers ten gevolge van epidemieŽn. Dodelijke ziekten waren er bij
de vleet in die tijd: pokken, cholera, dysenterie… Farr ontdekte dat de sterftegrafieken
vrijwel altijd een klokvorm hadden; ofwel: Gausskrommen waren. Hoe sneller de sterftecijfers
stegen, hoe sneller ze ook weer zouden dalen. What goes up, must come down.
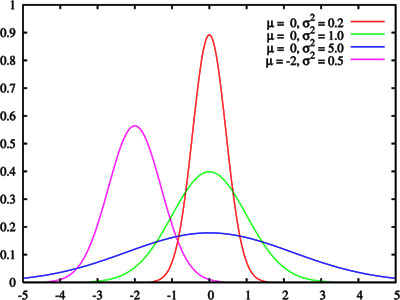
Gausskrommen. Ze dalen even snel als ze gestegen zijn.
Afbeelding overgenomen van Wikipedia: Karl Friedrich Gauss
Het ligt wel voor de hand, als je er even over doordenkt. Als
een epidemie heel snel om zich heen grijpt, vermindert ook het aantal
potentiŽle nieuwe slachtoffers van de ziekte zienderogen. Zijn er al veel
patiŽnten overleden, en veel anderen genezen en immuun geworden, dan moet de
epidemie wel een keer tot stilstand komen.
Ook gaan bij een grote piek in het aantal sterfgevallen verstandige
mensen drastische maatregelen nemen tegen verdere verspreiding. En ook daardoor
daalt het aantal nieuwe gevallen snel. Laten uitrazen was in vroeger eeuwen al
geen verstandige tactiek, en quarantainemaatregelen zijn zo oud als de wereld.
Het opmerkelijke van dit verhaal is dat William Farr
helemaal niet wist waardoor besmettingen veroorzaakt werden. Sterker nog: hij
gelůůfde zelfs niet in besmettingen.
In zijn tijd waren virussen nog volkomen onbekend. BacteriŽn
kende men wel, maar men wist nog niet dat het ziekteverwekkers waren. Louis
Pasteur zou dat pas in 1859 ontdekken.
Er heerste al eeuwenlang een controverse tussen artsen.
Sommigen hielden wel rekening met besmettelijkheid, overdracht van persoon op
persoon, al was het mechanisme erachter nog niet ontdekt. Maar Farr en veel van
zijn vakbroeders geloofden nog in miasma. Dat was de benaming voor bedorven, met
verrotte organismen verontreinigde lucht. Die zou een bron zijn van ziekten,
zoals malaria, wat letterlijk slechte lucht betekent.
Zonder iets te snappen van ziekteverwekkers, wist Farr wel
een wet op te stellen over hoe ze zich gedragen. Het gaat niet exponentieel,
maar in een klokvorm.
Maar of dat nu betekent dat we optimistisch kunnen zijn over
de omikron-golf: ik durf het niet te beloven.
FHM
26 december 2021
25 jaar
De thuispagina van Frans Mensonides: hoe het begon
